不用的东西学了总是会忘掉。我还是做点笔记吧。

废话

不得不说，课和课之间的差距真是不比人和人之间的差距小。

笔记

本文为学习Games 101过程中的随手笔记。很多内容之前各个来源了解过但欠缺系统连结和应用，慕名前来重修一遍。也因此笔记略过一些熟悉的内容，课程2倍速播放也记不了太多。

L2 线性代数回顾

没什么好说的。叉积用得实在不多印象模糊，记一些。

向量叉积

定义 & 性质

方向：右手定则
长度： $|a||b| \sin \theta$
交换律：$a \times b = - b \times a$
矩阵形式：

$$ a \times b = A^* b = \begin{pmatrix} 0 & -z & y\\ z & 0 & -x\\ -y & x & 0 \end{pmatrix} $$

应用

判断左右，叉积结果为正 （个人理解为再对$(1, 1, 1)$做一次混合积） 在左
判断点是否在图形内：各边依次叉积，判断是否同左或同右（光栅化基础）

基向量

也没什么好说的。但有一个有意思的恒等式： $$ 对于一组标准正交基\vec{i}, \vec{j}, \vec{k} \\ \vec{p} = (\vec{p} \cdot \vec{i})\vec{i} + (\vec{p} \cdot \vec{j})\vec{j} + (\vec{p} \cdot \vec{k})\vec{k} $$

原理上是显然的：向量分别投影(内积)到各个基向量再乘以该基向量，最后加总组成原向量。但线性代数的证明没有想清楚。但对于任意维度，掰成解析几何用代数方法证明应该也是显然正确的。

L3 变换

放缩、反射略过，旋转后面说

Shear 切变一维度不变另一维度放缩比例与前一维度线性相关。横拉平行四边形。

以上均为线性变换

旋转矩阵

定义

$$ \begin{pmatrix} \cos{\theta} & -\sin{\theta}\\ \sin{\theta} & \cos{\theta} \end{pmatrix} $$

性质

旋转矩阵$A$，是一个正交矩阵。这意味着$A^T = A^{-1}$。

正交矩阵

正交矩阵共有两类，旋转是其第一类，行列式为1；另一类行列式为-1。
正交矩阵是各个向量都互相正交，构成一组正交基的矩阵。由此产生的变换可以认为是转换正交基的一类变换。在这类变换中，坐标原点不变，向量长度不变；你也可以说各点之间的欧氏距离不变。

正交变换

直接正交矩阵直接放向量左乘即可变换到该组正交基。 $$ 将任意正交矩阵A表达为 \begin{pmatrix} \vec{i} \\ \vec{j} \\ \vec{k} \end{pmatrix} ，则A \vec{x} = \begin{pmatrix} \vec{i} \cdot \vec{x} \\ \vec{j} \cdot \vec{x} \\ \vec{k} \cdot \vec{x} \end{pmatrix} $$

这熟悉的内积投影，同理于之前基向量一节所提到的公式。

应用

由于正交矩阵的性质，当求旋转矩阵不好求时，可以先求逆矩阵后做转置。

齐次坐标 Homogeneous Coordinates

动机

事实上齐次坐标的引入还见过其他更多的解释和优势，比如表示无穷远点，符合透视原则等，但想不全了。这里只介绍了一个主要原因：统一平移变换。

设计

增加一个维度：

向量： $(x, y, 0)$
点： $(x, y, 1)$

平移表示为 $$ \begin{pmatrix} 0 & 0 & t_x\\ 0 & 0 & t_y\\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x\\ y\\ 1 \end{pmatrix} $$

从而有：

向量+向量=向量
点-点=向量
点+向量=点
点+点=中点

对于点$(x, y, w)$，其与$(x/w, y/w, 1)$表示同一个点。

仿射变换 Affine Transformations

词源

中文似乎是胡逼音译过来的……英文中代表很像，与congruency, similarity成递进关系，转换前后空间中保持平行关系，距离保持比例关系。

定义

线性变换+平移

L4 三维变换

视图/相机变换 View/Camera Transformation

事实上就是求一个ModelView Transformation Matrix。

习惯上把摄像机放在坐标原点，指向-z方向，顶端指向y方向，由此三个约束唯一确定摄像机姿态。同时将世界中的物体依同样变换转移坐标系。

变换组合为$R T$，即先平移到坐标原点，再进行旋转（左乘规则，右侧T先被计算）。平移简单，齐次第四列加上平移差量即可。旋转时先考虑逆变换：目标空间中单位基向量经过怎样的变换$R^T = R^{-1}$到当下空间中的基向量。

$$ Current base: (\vec{g \times t}, \vec{g}, \vec{t})^T \\ Target \vec{x} = (1, 0, 0)^T, so the first column is (x_{\hat{g} \times \hat{t}}, y_{\hat{g} \times \hat{t}}, z_{\hat{g} \times \hat{t}})^T $$

然后再求个逆得到 $$ \begin{pmatrix} x_{\hat{g} \times \hat{t}} & y_{\hat{g} \times \hat{t}} & z_{\hat{g} \times \hat{t}} \\ x_t & y_t & z_t \\ x_{-g} & y_{-g} & z_{-g} \end{pmatrix} $$

个人理解倒也不必这么麻烦。根据前面正交变换这里的理解，要想转换单位正交基到一组新的正交基，直接左乘一个由新正交基构成行向量的正交矩阵就可以了，这样可以直接得出所需的$R$。

由此，我们得到了MV矩阵。

投影变换 Projection Transformation

正交投影 Orthographic Projection

简单的理解
- 摄像机仍然这么摆放
- 丢弃Z轴
- 平移并缩放到$[-1, 1]^2$平面
图形学操作
定义标准立方体，将$[l, r] \times [b, t] \times [f, n]$映射到标准(canonical)立方体$[-1, 1]^3$
- 注意到由于右手坐标系，我们沿-z方向观察，因此远(far)的z值更小，处于闭区间左端
  
  因此OpenGL等使用左手系，使得far > near更直观
- 很显然的，我们得到以下变换矩阵(先平移(右侧)，再缩放(左侧))（不过先缩放好像也未尝不可？平移矩阵变成一个常量）
  $$ M_{ortho} = \begin{pmatrix} \frac{2}{r-l}&0&0&0\\ 0&\frac{2}{t-b}&0&0\\ 0&0&\frac{2}{n-f}&0\\ 0&0&0&1 \end{pmatrix} \begin{pmatrix} 0&0&0&-\frac{r+l}{2}\\ 0&0&0&-\frac{t+b}{2}\\ 0&0&0&-\frac{n+f}{2}\\ 0&0&0&1 \end{pmatrix} $$

透视投影 Perspective Projection

尝试将棱台frustrum *（但愿我没拼错）*通过线性变换挤压成长方体，再应用正交投影。

首先通过切面的相似三角形，可以得到x, y的缩放系数为$n/z$。即任意一齐次坐标$(x, y, z, 1)$应用挤压变换后映射到$(nx, ny, ?, z)$。显然该矩阵有以下形式：

$$ \begin{pmatrix} n&0&0&0\\ 0&n&0&0\\ ?&?&?&?\\ 0&0&1&0 \end{pmatrix} $$

注意到以下两种特殊解/约束条件：

近平面上所有点映射到自身
远平面上所有点映射到相同平面上，且中心点映射到自身

可以得到所要求的变换矩阵为 $$ M_{perspective2ortho} = \begin{pmatrix} n&0&0&0\\ 0&n&0&0\\ 0&0&n+f&-nf\\ 0&0&1&0 \end{pmatrix} $$

则完整变换 $$ M_{projection} = M_{orthographic}M_{perspective2ortho} $$

思考问题

远近平面深度不变，那么之间的点呢？

应该是变远了(更接近远平面)。尝试证明如下：

对于其中任意一点$(x, y, z, 1)$，变换后坐标为$(nx, ny, (n+f)z-nf, z)$，深度值为$n+f-\frac{nf}{z}$。

$$ z - (n+f-\frac{nf}{z}) = z + \frac{nf}{z} - (n+f),\ z \in [f, n] \\ \because z + \frac{nf}{z} \text{is convex with a minimum value}\ 2 \sqrt{nf}, \text{maximum value}\ n+f\\ \therefore z \le n+f-\frac{nf}{z} \ \blacksquare $$

但我很好奇这到底是怎么样的一个变换，拿Python简单画了个图。[10, 100]，等距蓝色直线经过变换后到红色。还是挺大的一个挤压。

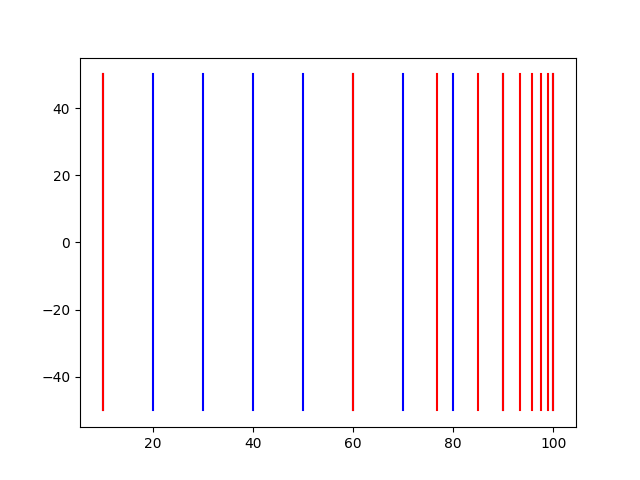
蓝色直线变换后为红色

原本想象的是Z不变。尝试写一个期望的Z不变的变换矩阵发现不太行。由于x, y压缩时带入了z变量，导致要保证这矩阵是齐次的话z也要带入一个1/z的系数，从而变换矩阵只能唯一是我们求到的这个。所以约束条件可以多一个：变换矩阵得是齐次的。

L5 光栅化（三角形） Rasterization (Triangles)

视口变换

保持z不变，x,y扩展到视口大小。$[-1,1]^2$到$[0, width] \times [0, height]$。

视口变换矩阵： $$ M_{viewport} = TS = \begin{pmatrix} \frac{width}{2} &0&0&\frac{width}{2}\\ 0&\frac{height}{2}&0&\frac{height}{2}\\ 0&0&1&0\\ 0&0&0&1 \end{pmatrix} $$

三角形

使用三角形作为片元的优点：

保证同一平面
易插值
方便判断内部

光栅化

光栅化本质是使用inside函数（判断点是否在三角形内）在屏幕空间进行采样。还是上次说的使用外积判断点是否在内部。

对于每一个图形通过取包围盒减少计算量。简易片元包围盒取三个顶点的$x_{min}, y_{min}, x_{max}, y_{max}$组成矩形四个顶点。

反锯齿（Anti-aliasing）是一个重要问题。

L6 光栅化（抗锯齿和Z-buffering） Rasterization (Antialiasing and Z-Buffering)

抗锯齿

采样是图形学常见(Ubiquitous)概念。同样走样(Aliasing)也是。采样误差被称为Sampling Artifacts。

锯齿 (Jaggies)：空间采样误差
摩尔纹 (Moire)：图像欠采样
电风扇倒转 (Wagon wheel effect)：时间采样误差
…

原因：高频信号采样频率不够

抗锯齿采样

模糊预处理（低通滤波），过滤掉奈奎斯特 (Nyquist) 极限以上的信号。

图像高频信息通常表达边界，低频缺少细节。

傅里叶变换

时域的卷积 = 频域的乘积时域的乘积 = 频域的卷积

采样 = 冲激函数 * 原始函数
因此在频域上采样 = 冲激函数频率卷积原始函数频域
因此采样在频域就是重复原始信号频谱。

抗锯齿方法

增加采样率（增大分辨率）不太行（硬件改动）
过滤高频信号行！

MSAA Multi Sampling AA

像素内超采样，取平均值。超采样得到近似三角形覆盖，实现模糊步骤。成倍增加计算量。

FXAA Fast Approximate AA

找出锯齿边界并替换。

TAA Temporal AA

复用上一帧信息。

L7 着色（光照，着色和渲染管线） Shading (Illumination, Shading and Render Pipelne)

接上节未完成的深度测试。

深度测试

画家算法

从远到近覆盖绘制。存在不可解的深度关系，如三个物体互相交错。

深度缓存

正想问MSAA的深度缓存怎么做，没想到是作业。待会儿看一下。猜一下是把深度缓存扩大到超采样点，之后计算覆盖值应该在最后一步。想想都觉得很合理，接近的两个超像素会混合颜色。emm~满意。

透明物体不参与Z-Buffering。

着色

Blinn-Phong Reflectence

模型定义光照 = 高光 (Specular) + 漫反射 (Diffuse) + 环境光 (Ambient)

着色是局部 (local) 的。只考虑本身，不考虑其它元素（阴影）。

有以下4个属性：

入光方向$l$
法向量$n$
视线方向$v$
其他属性（shiness, color ,…）

漫反射

Lambert cosine law
能量守恒看，光方向与片元面法向量夹角决定片元收到的能量强度
Light falloff
能量守恒看，点光源辐射能量强度与距离平方反比（类比电磁场/引力）

$$ L_d = k_d \frac{I}{r^2} \max(0, \hat{n} \hat{l}) $$

漫反射与观察角度无关。

L8 着色（着色，管线和纹理映射） Shading (Shading, Pipeline and Texture Mapping)

继续Blinn-Phong模型

着色

Blinn-Phong Reflectence Cont.

高光

越接近出射光方向越亮。做一个减少计算量的优化：v越接近出射光方向同时也意味着v与l的 半程向量 h越接近法线n。h所需计算量比出射光小。 $$ \vec{h} = \frac{\vec{l} + \vec{v}}{|\vec{l} + \vec{v}|} $$

$$ L_s = k_s \frac{I}{r^2} \max(0, \hat{n} \hat{h})^p $$

指数$p$使得cosine函数更陡峭，高光反射范围更窄。高光一般取白色。

环境光

$$ L_a = k_a I_a $$

加总

$$ L = L_a + L_s + L_d $$

着色频率

flat shading: 对每个三角形求法线并统一着色
Gouraud shading: 对顶点着色并插值
Phong shading: 插值法线向量并对每个像素着色 （与光照模型不是同一概念）

当面数增大时，他们之间是一个trade-off。面数超过像素数，或许Phong shading更省资源。

顶点法线

周围面法线（加权）求平均。

像素法线

顶点法线插值。

实时渲染管线

输入：三维空间顶点
顶点处理：投影到屏幕空间
三角形处理：形成三角形
光栅化：形成离散片元
片元(Fragment)处理：着色片元
帧缓存操作：输出到屏幕

顶点、片元可编程。除此外出现更多的可编程shader比如geometory（可增加三角形）、computing（通用计算）。

纹理映射

几何参数化问题（none of our business）

L9 着色（纹理映射） Shading (Texture Mapping cont.)

纹理映射

重心坐标 Barycentric Coordinates

一种三角形的坐标系统

三角形ABC中，任意点$(x,y)$可以表示为$\alpha A + \beta B + \gamma C$，其中$\alpha + \beta + \gamma = 1$。对于三角形内任一点，三个参数非负。

参数计算可以使用三角形面积比。（叉积）

重心坐标在投影中并不是不变的。因此三维空间插值应在三维空间中完成后再投影。

纹理放大 Texture Magnification

最近邻
双线性插值 Bilinear Interpolation: xy方向最近四个texel简单线性插值
双立方插值 Bicubic：最近16个texel线性插值

纹理过大

Mipmap

生成分辨率 1/4的多个纹理，额外占1/3空间

三线性插值 +层与层之间插值

各向异性过滤 Anisotropic Filtering

Ripmap解决矩形区域采样问题，但更多异形无法解决（如斜着采样），可借助EWA等花费更多代价解决。

L10 几何 Geometry (Introduction)

纹理映射 cont.

其他应用

环境光照球状贴图 -> cubic map
法线贴图: 计算相邻贴图位置高度差，新向量垂直于计算得到的梯度
位移贴图 Displacement mapping：真实移动顶点，不会在边缘/阴影露馅
要求三角形定义比纹理更细。可联合动态细分 Dynamic tasellation应用。

几何

隐式几何：使用点满足的关系表示几何
包括解析式、距离函数（可以由离散grid-stored value表示）
显示几何：通过直接给出点或使用参数映射 *(parameter mapping)*的方式
With a mapping and function $f: \mathbb{R}^2 \rightarrow \mathbb{R}^3; (u,v)\mapsto (x,y,z)$

隐式几何

优点：
- 紧实(compact)的表示
- 特定查询方便（内部性判断、到表面距离）
- 易于线面相交计算
- 简单形体无采样误差
- 易于处理拓扑变换
缺点：
- 不易描述复杂形体

L11 几何（曲线和面） Geometry (Curves and Surfaces)

显式几何

点云
多边形 meshes
参数映射贝塞尔曲线

贝塞尔曲线 Bezier Curves

性质

端点插值
Tagent to end segments
仿射变换特性：变换后的曲线与仿射变换后的控制点的到的贝塞尔曲线一致
曲线在控制点所在的凸包 (convex hull) 内

日常应用中常用四个控制点（钢笔工具）多个分段曲线组成长段光滑曲线。对齐连接点控制点共线并等长距离可做到C0光滑（一阶导数一致）

样条 spline

一条穿过各个控制点的曲线

B(basis)-splines

相比贝塞尔曲线需要更多信息
满足所有贝塞尔曲线性质，是其超集
局部性

较为复杂，不为展开。另有非均匀有理B样条(NURBS)。同时曲线操作也不为展开。

相关展开内容可以参考Prof. Shi-Min Hu’s course。

贝塞尔曲面

二维下如同双线性插值，一个方向上的控制点定义了一组平行贝塞尔曲线；再对平行贝塞尔曲线在另一个方向上取值认为是一组最终控制点，定义了在另一个方向上连续的一组贝塞尔曲线，从而组成曲面。

我猜测维度方向的选择应该和最终结果无关。但不是很想证明。本质上贝塞尔曲线是多次线性插值的结果，这个性质应该是符合直觉的。

面操作

面细分 subdivision
面简化 simplification
面正规化 regularization

L12 几何 Geometry

首先骄傲了下CG第二次获得图灵奖，并炫耀了一下“科研族谱” (What’s that?!) 获得图灵奖的是Prof. Yan握过手的师爷 (还是值得骄傲的恭喜恭喜。这么算我祖师爷拿了图灵奖，与有荣焉🤪)

面细分

Loop Subdivision (三角形面)

连接三角形各边中点得到细分三角形。
新顶点位置 = 3/8 两近顶点位置 + 1/8 两远顶点位置
旧顶点位置更新 = (1 - n*u)本顶点原位置 + u邻居顶点位置和，n为顶点的度，u = n==3 ? 3/16 : 3/(8n)

Catmull-Clark Subdivision (General Mesh)

不要求全是三角形面。

奇异点(Extrodinary Points)指度不为4的顶点。对每个非四边形面，取面上中点，连接周围边上中点。其余连接边上中点。经过一次细分后会产生非四边形面数量的奇异点。此后所有面变为四边形面。

面上的点：$f = \frac{v_1+v_2+v_3+v_4}{4}$
边上的点：$f = \frac{v_1+v_2+f_1+f_2}{4}$
原先顶点：$v = \frac{f_1+f_2+f_3+f_4+2(m_1+m_2+m_3+m_4)+4p}{16}$

面简化

Collapsing edges

边坍缩。将一条边去除，连接两端顶点。

误差度量：二次误差

最小化新点到原先各个面的距离平方和。

边选择

对所有边求二次误差最优值，依次选择最小误差边进行坍缩。(Garland & Heckbert 1997)

动态更新局部受坍缩影响的点。堆。

Shadow Mapping

对点光源而言，不在阴影中的点 = 能被摄像机看到 && 能被点光源看到。（传统阴影映射只能处理点光源）

从光源看向场景，记录深度
从摄像机看向场景，对每个点投影回光源记录的平面，检测光源深度缓存是否与当前深度一致

问题：

硬阴影only（点光源）
质量依赖shadow map分辨率
引入浮点数相等比较带来的精度问题

软阴影

是由于光源存在大小而非点光源引起

L13 光线追踪 Ray Tracing

假设

光沿直线传播
光不会碰撞
光从光源到眼睛（但光路是可逆的 (reciprocity) ）

Whitted-Style Ray Tracing

从视点发射光线，递归。每次碰撞判断交点与光源可见性，求着色。

Ray-Surface Intersection

Ray Equation

$$ r(t) = o + t\vec{d}, 0 \le t \le \inf $$

隐式表示求交

代入函数求解。发达的数值方法不用担心求不出来。

显示表示求交（三角形面）

对每个三角形求交？（加速方法卖个关子之后再讲）

求交方法

分解成两步

与三角形所在平面求交点
判断交点是否在三角形内

平面法线$N$，任意一点$p^{\prime}$，平面点法式$(p-p^{\prime})\cdot N = 0$。带入射线方程解得

$$ t = \frac{(p^{\prime} - o) \cdot N}{d \cdot N},\ t \in [0, \inf) $$

Molller Trumbore Algorithm

更快的方法。利用重心坐标解以下线性方程组：

$$ O+tD = (1-b_1-b_2)P_0+b_1 P_1 + b_2 P_2 $$

得到重心坐标后可以立刻判断是否在三角形内。

求交加速

包围体积 Bounding Volumn

三维长方体包围盒：认为由三对平行平面(pairs of slabs)组成的交集（轴对齐包围盒(Axis-Aligned Bounding Box (AABB))）

对每一组对面都求一个进入时间和离开时间。光线在盒子内的时间为$[\max(t_{enter}), \min(t_{exit})]$。

有以下特殊情况需要处理：

$t_{exit} \lt 0$：盒子在后面，无交点
$t_{exit} \ge 0, t_{enter} \lt 0$：在盒子内

当且仅当$t_{enter} \lt t_{exit}, t_{exit} \ge 0$时有交点。

平行于轴的光线怎么办？

L14 光线追踪 Ray Tracing

求交加速 cont.

网格法 Uniform Grids

将场景划分为网格组成包围盒指示内部是否存在物体边界。

空间划分 Spatial Partition

八叉树 Oct-Tree
KD-Tree
BSP-Tree

KD-Tree is preferred. 但由于多边形求交困难，渐渐不用。一个物体同时可能存在多个盒子内。

物体划分 Object Partition & Bounding Volume Hierarchy (BVH)

将集合中物体分成两份（按空间划分）各自计算包围盒。启发式延长轴划分。启发式按中间位置物体划分。寻找中位数是一个O(n)算法。改一改快排就行了。

伪代码

void intersect(Ray ray, BVH node) {
    if (ray misses node.bbox) return;
    if (node is a leaf node) {
        test all objs;
        return closest intersection;
    }

    hit1 = intersect(ray, node.child1);
    hit2 = intersect(ray, node.child2);
    reuturn closer of hit1, hit2;
}

辐射度量学 Basic Radiometry

学物理可太快乐了

光的空间属性

radiant flux 辐射通量
intensity 辐射强度
irradiance
radiance

Radiant Energy and Flux (Power)

energe Q in J(oule)
flux (power) $\Phi \equiv \frac{dQ}{dt}$ in W(att) / lm (lumen)

Important Light Measurements of Interest

light emitted from a source: radiant intesity
light falling on a surface: irradiance
light traveling along a ray: radiance

Radiant Intensity

power per unit solid angle(立体角): $I(\omega) \equiv \frac{d \Phi}{d \omega}$ in candela, W or lm divided by solid angle.

坎德拉是基本单位之一，代表光亮度，光亮度与能量不是同一概念。可能是借用？

Solid Angle

立体角度对应球面面积除以半径平方. 球面立体角4pi.

$$ dA = (rd \theta)(r \sin \theta d \phi) = r^2 \sin \theta d \theta d \phi \\ d \omega = \frac{dA}{r^2} = \sin \theta d \theta d \phi $$

$\theta$作为纵向角，$\phi$作为横向角，两者定义方向向量$\omega$。

各向同性点光源 Isotroppic Point Source

$$ \Phi = \int_{S^2} Id \omega = 4\pi I \\ I = \frac{\Phi}{4\pi} $$

L15 光线追踪 Ray Tracing

Irradiance

Power per unit area. 光线垂直打到表面上。

$$ E(x) = \frac{d\Phi(x)}{dA} $$ 单位lux(lm/m^2)

Radiance

Power emitted/reflected/transmitted/received by a surface, per unit solid angle, per projected unit area. 理解为单位面积朝单位立体角辐射/被辐射的能量（此处指功率，下同）

$$ L(p, \omega) \equiv \frac{d^2\Phi(p, \omega)}{d\omega dA\cos\theta} $$

单位nit(cd/m^2)

Bidirectional Reflectance Distribution Function (BRDF)

表示从每个入射角反射到每个出射角的光线量

$$ f_r(\omega_i \rightarrow \omega_r) = \frac{dL_r(\omega_r)}{dE_i(\omega_i)} = \frac{dL_r(\omega_r)}{L_i(\omega_i)\cos\theta_id\omega_i} $$

单位1/sr。个人理解可以理解为对于一个出射方向能量，各个入射方向的贡献分布。

反射方程 Reflection Equation

对于特定观察方向（出射角），辐射光量为

$$ L_r(p, \omega_r) = \int_{H^2}f_r(p, \omega_i\rightarrow\omega_r)L_i(p, \omega_i)\cos\theta_id\omega_i $$

这个方程是递归求解的。麻烦。

渲染方程 Rendering Equation

增加一个发射光量。得到

$$ L_o(p, \omega_r) = L_e(p, \omega_o) + \int_{\Omega^+}L_i(p, \omega_i)f_r(p, \omega_i, \omega_o)(n\cdot\omega_i)d\omega_i $$

即渲染方程。

已知发射intensity，BRDF，入射角度，可以将式子简写为

$$ \begin{aligned} I(u) &= e(u) + \int I(v)K(u,v)dv \\ \implies L &= E + KL \end{aligned} $$

其中K为equation kernel，Light Transport Operator。这是一个经典形式的第二类Fredholm积分方程：有良好的数值解。

艹，接下来开始不明所以但很有道理的……泛函分析？PDE？还是基于什么别的东西的推导。函数当矩阵算好爽啊。以及一个二项展开。这级数收敛性……据说是收敛的。

$$ \begin{aligned} L&=E+KL\\ IL-KL&=E\\ (I-K)L&=E\\ L&=(I-K)^{-1}E\\ L&=(I+K+K^2+K^3+\ldots)E\\ L&=E+KE+K^2E+K^3E+\ldots \end{aligned} $$

我们得到了一个级数。第一项为光源直射，第二项为直接光照，第三项为弹射一次的间接光照，之后为更多次的间接光照。作为经典光栅化着色，我们得到的是光源直射和直接光照的近似（近似到前两项）。

概率论回顾

概率论还没忘那么多，不多回顾了

$$ X \sim p(x)\\ Y = f(X) \\ E[Y] = E[f(X)] = \int f(x)p(x)dx $$

L16 光线追踪（蒙特卡洛路径追踪） Ray Tracing (Monte Carlo Path Tracing)

蒙特卡洛积分 MC

对$\int f(x)dx$的求解可以通过抽样近似。设抽样随机变量$X \sim p(x)$，则

$$ \int f(x)dx \approx \frac{1}{N}\sum^N_{i=1}\frac{f(x_i)}{p(x_i)} $$

路径追踪 Path Tracing

从而我们可以通过MC解渲染方程。对于表面以上各方向入射光线积分，每次随机选择n个方向求均值。理论完备，但实现中有以下问题：

MC采样数指数上升
递归求解没有递归终点
采样数减少导致结果噪点较大

路径追踪优化

对于采样数指数上升问题，将采样数限定为1可避免增长。进行多次Tracing求均值。

递归终点若简单限制步长会造成能量损失。通过“俄罗斯轮盘赌”方法每次以一定概率结束采样，同时对接受的采样除以概率p，可使得最终能量的期望仍守恒。

在有限的采样数内，若使用均匀采样会有较多的结果miss直接光照，样本无效率较高。提高采样效率，通过选取另一种MC采样分布实现。
采样分为光源采样及间接光照采样。光源通过将积分微元从$dw_i$转换到$dA$，即选取有效物体表面进行采样，规避无效采样。微元间有以下关系（$dA$乘以$\cos\theta^\prime$得到平行于反射面面积，剩余部分相似三角形易证）

$$ dw_i = \frac{dA\cos\theta^\prime}{\|x-x^\prime\|^2} $$

其中$\theta^\prime$为入射光线（光源的出射光线）相对于光源平面法线的角度。
间接光照维持球面随机采样，轮盘赌结束递归的方式。
采样微元转换到光源平面后，需要解决光源是否被遮挡问题。从着色点cast ray到光源微元点，看是否被遮挡。

路径追踪结束。

路径追踪处理点光源上有点麻烦。大概是点光源没有面积的原因，采样受到了干扰。这是点光源的问题🐶 考虑做成小面积光源。

路径追踪的一些Topic

重要性采样：MC采样分布的优化
多重重要性采样：结合半球采样与光源采样
像素重建滤镜：像素radiance不必是所有穿过它的路径的均值
伽马矫正/色彩空间：像素的radiance不必是像素的颜色
抽样方法的选择
随机数的选择：low discrepancy sequences
除路径追踪外的其他方法：
- 光子映射 photon mapping
- 双向路径追踪
- Metropolis light transport
- VCM / UPBP
- …

他保证难的都过去了。这个梯度可真好。可能老师期望不是很高吧hhhh

L17 材质与外观 Materials and Appearances

Material = BRDF

漫反射材质 Diffuse/Lambertian Material

假设入射光线是均匀的，在各个方向上都是常数
这个假设其实没有很确信起因。模型上来讲只能说因为漫反射出射光与入射光无关，因此做这么个假设简化计算。但如此BRDF分布就被大大简化了……不过确实变得可解了。 本来一直好奇BRDF这么个复杂的二维概率分布该怎么实现，所以BRDF最后还是会退化么。 $$ \begin{aligned} L_o(\omega_o) &= \int_{H^2}f_rL_i(\omega_i)\cos\theta_id\omega_i \\ &= f_rL_i\int_{H^2}\cos\theta_id\omega_i \\ &= \pi f_rL_i \end{aligned} $$

可知$f_r = \frac{1}{\pi}$时能量守恒，完全反射入射光。定义$f_r = \frac{\rho}{\pi}$，$\rho$为反射率（albedo(color)），在0到1之间。

完全镜面反射 Perfect Specular Reflection

平行四边形法则得出射角，方位角180度。

折射 Refraction

斯涅耳定律

$\eta_i\sin\theta_i = \eta_t\sin\theta_t$ $$ \begin{aligned} \eta_i\sin\theta_i &= \eta_t\sin\theta_t \\ \cos\theta_t &= \sqrt{1 - \sin^2\theta_t} \\ &= \sqrt{1-(\frac{\eta_i}{\eta_t})^2\sin^2\theta_i} \\ &= \sqrt{1-(\frac{\eta_i}{\eta_t})^2(1 - \cos^2\theta_i)} \\ \\ 1-(\frac{\eta_i}{\eta_t})^2(1 - \cos^2\theta_i) \ge 0 \end{aligned} $$

菲涅尔项 Fresnel Term

反射性和法线夹角、光线极化有关。法线夹角越大，反射性越强，反射能量越多。（玻璃越斜看越不透明）

导体绝缘体菲涅尔项不同。

$$ R_s = \left|\frac{n_1\cos\theta_i-n_2\cos\theta_t}{n_1\cos\theta_i+n_2\cos\theta_t}\right|^2 \\ R_p = \left|\frac{n_1\cos\theta_t-n_2\cos\theta_i}{n_1\cos\theta_t+n_2\cos\theta_i}\right|^2 \\ R_{eff} = \frac{R_s+R_p}{2} $$

Schlick’s approximation

$$ R(\theta) = R_0 + (1-R_0)(1-\cos\theta)^5 \\ R_0 = (\frac{n_1-n_2}{n_1+n_2})^2 $$

微表面模型 Microfacet Material

近处是几何，远处是材质。使用微表面材质得法线分布来定义材质。glossy法线分布相对集中，diffuse法线分布相对分散。

$$ f(i,o) = \frac{F(i,h)G(i,o,h)D(h)}{4(n,i)(n,o)} $$ F为菲涅尔项，G为自阴影项（shadowing-masking term），D为法线分布。平射光线(掠射角度Grazing Angle)更容易被自阴影挡住。

各向同性/异性材质 Isotropic/Anisotropic Materials (BRDFs)

没说怎么模拟解决，只提了几个case。

BRDF的若干性质

非负性
线性：指线性可加，可分为不同部分分别计算后相加（Blinn-Phong的正确性来源）
可逆性：交换入射出射方向，数值完全一致
能量守恒：BRDF给定出射角，对所有入射角积分，值小于等于1：保证了光追收敛
各向同性与各项异性
- 各向同性中$f_r(\theta_i,\phi_i;\theta_r,\phi_r) = f_r(\theta_i,\theta_r,\phi_r-\phi_i)$，四维降为三维函数
- 由可逆性可知
  $f_r(\theta_i,\theta_r,\phi_r-\phi_i)=f_r(\theta_r,\theta_i,\phi_i-\phi_r)=f_r(\theta_i,\theta_r,|\phi_r-\phi_i|)$

测量BRDF

Image-based: Gonioreflectometer / spherical gantry
材质存储：耗空间大。MERF BRDF Database可供参考。存储压缩是一个时兴话题。

L18 高阶渲染话题 Advanced Topics in Rendering

高级光线传播 Advanced Light Transport

无偏光线传播方式 Unbiased light transport methods
- Bidirectional path tracing (BDPT)
- Metropilis light transport (MLT) named after inventor
有偏光线传播 Biased light transport methods
- Photon mapping 光子映射
- Vertex connection and merging (VCM) 光子映射+双向路径追踪
Instant radiosity 实时辐射度 (VPL/ many light methods)

Biased vs. Unbiased Monte Carlo Estimators

无偏(Unbiased)估计期望值始终等于真实值，无系统性误差
否则有偏(Biased)
- 当期望值随样本数增多收敛到真实值，则它是一致的(Consistent)

双向路径追踪 (BDPT)

从光源与摄像机分别进行子路径追踪。

如果在光源处光线路径复杂，则效果较好
难以实现，速度慢

Metropolis Light Transport

使用马尔科夫链(MCMC)进行采样
- 以一定概率分布从当前采样点寻找到下一个采样点
擅长局部探索一些困难的光路
关键思想
- 局部扰动一条现存的路径以获得新的路径
优点
- 适合解决复杂光路 (e.g. caustics)
- 无偏
缺点
- 难以估计收敛率
- 不保证每个像素有相同的收敛率
- 常常产生“脏的”结果
- 不常被使用于动画渲染

Photon Mapping 光子映射

有偏方法 & 两步方法
非常善于处理Specular-Diffuse-Specular(SDS)路径并产生焦散(caustics)

大致框架：

光子追踪 photon tracing
从光源发射光子，弹射，记录光子最后落在的diffuse表面
光子收集 photon collection
从摄像机发射子路径，弹射，直到击中diffuse表面
计算局部密度估计 (local density estimation)

思想：拥有越多光子的区域越亮
对每个着色点，寻找最近N个光子，取其覆盖面积，计算密度
- 如：最近着色点取包围球，求球体在着色面上的相交面积

有偏的原因

局部密度估计中$dN/dA \neq \Delta N/\Delta A$

当光子无限多时，以上估计收敛到真实值。因此本方法一致(Consitent)。

渲染中一般来说

有偏方法产生模糊的结果
一致方法在样本数无穷大时变得清晰

当使用固定大小区域估计光子密度时，由于$dA$永远不会变小，因此将永远是一个有偏估计，并且不一致。

VCM

结合双向路径追踪和光子映射

关键思想
- 不浪费双向光追中的子路径当追踪终点无法被连接但可以被融合时（指在一个面上邻近）
- 使用光子映射来融合邻近光子

电影行业运用广泛

Instant Radiosity

有时被称为many-light方法
关键思想
- 被照亮的表面可以被认为是光源
方法
- 发射子光路并认为每条光路的终点都是一个虚拟点光源（Virtual Point Light）
- 使用虚拟点光源渲染场景
优点
- 速度快，在漫反射表面有不错的效果
缺点
- 当虚拟点光源接近着色点时会有spikes（异常发光）出现
  - 类比直接光源采样，对立体角的采样转化为对光源面积采样除以距离。当距离平方项极小，结果被异常放大。
- 无法处理光滑(glossy)物体

高阶外观建模 Advanced Appearance Modeling

非表面模型 Non-surface models
- 散射介质 Participating media
- 毛发纤维 (BCSDF)
- 颗粒材质 Granular material
表面模型 Surface models
- 半透明材质 Translucent material (BSSRDF)
- 布料 Cloth
- 细节材质 Detailed material (non-statistical BRDF)
生成外观 (Procedral appearance)

散射介质

光线穿过散射介质中的任何时候，它都会（部分）被吸收和散射
使用相位函数（Phase Function) 来描述在散射介质中任意点光线在各个角度上的散射分布

散射介质渲染方法

随机选择弹射方向
随机选择直射距离
在每一个着色点，连接光源

毛发

有两种高光

Kajiya-Kay 模型

考虑了圆柱体近似下一定角度的散射+漫反射

Marschner 模型

将光线分为三部分

圆柱体直接反射R
穿入头发再穿出TT
穿入头发，内部反射后再返回穿出TRT

头发建模为玻璃样圆柱，外层cuticle，内层cortex。

结果真实。多次反射效果很好。计算量大。

双圆柱模型 Double Cylinder Model (Yan model)

听闫老师讲自己的work。（其实对我感觉人毛发模型用动物上去还是蛮可以接受的了，就是那示例狼脑袋黑了点）

新增一个毛发髓质(Medulla)的研究。髓质散射光线。动物毛发相比人有更大的髓质。

相比M模型，新增两个光线分类：原先穿过头发的两类光线受髓质影响新增TRTs & TTs。

猩球崛起和狮子王都有采用该毛发模型。均获得奥斯卡最佳视觉效果提名。

颗粒模型

分颗粒成分比例进行渲染。没有得到很好的解决。

表面模型半透明材质

E.g. 玉石、水母。

次表面反射 Subsurface Scattering

Scattering Functions

BSSRDF: BRDF的延申；一点出射光线受另一点入射光线影响$S(x_i, \omega_i, x_o, \omega_o)$

渲染方程的泛化：对表面的所有点和所有方向积分 $$ L(x_o, \omega_o) = \int_A\int_{H^2}S(x_i,\omega_i,x_o,\omega_o)L_i(x_i,\omega_i)\cos\theta_id\omega_idA $$

Dipole Approximation

近似方法：通过引入两个点光源来近似次表面反射。

适合皮肤渲染。

布料

缠绕纤维的集合
两级缠绕
- 纤维(Fiber)缠绕成股(Ply)
- 股缠绕成线(Yarn)
线被纺(Woven)或织(Knitted)成不同布料。
给定纺织pattern，计算整体behavior

使用BRDF渲染

基本操作。但天鹅绒布料不是一个表面，不太合适。

布料：作为散射介质渲染

单独纤维的性质与分布转换为散射参数
当作散射介质渲染

布料：作为实际纤维渲染

如同毛发渲染。很好的效果，很大的计算量。

复杂外观

动机：渲染过于完美

闫：博士几年做了一点微小的贡献，大概是三件事：细节渲染是一个，毛发模型是一个，实时光追是一个

主要展示了下效果。原理听着大概是对于微表面模型的法线分布做了改进，取法线贴图一个周围区域内计算法线pdf，以避免朴素光追在微表面很难追踪到反射到光源的光路的尴尬。

近来潮流：波动光学

将光学卷到波动光学去。考虑光的干涉。涉及到复数域积分，跳过了实现未谈。效果确实很惊叹。例如磨砂铝表面放大看并不是纯白光，而是包含各种颜色杂光，但整体呈现白色。

程序化生成外观 Procedural Appearance

通过噪声函数实时生成纹理。

L19 摄像机、透镜与光场 Cameras, Lenses and Light Fields

独立话题。《现代摄影入门》。

成像 (Imaging) = 合成 (Synthesis) + 捕捉 (Capture)

为何相机需要透镜/小孔(pinhole)？
- 因为sensor收集记录irradiance，并不区分来源方向。去掉透镜/小孔后所有像素的irradiance相似（对各方向积分后的光照度结果）
针孔相机是光线追踪的模型
- 针孔相机的结果是没有景深的。各点成像结果都是锐利的。

焦距对视场的影响

对于固定的传感器尺寸，焦距减小，视场增大.$FOV = 2 \arctan(h/2f)$

因为历史原因，通常使用基于35mm胶片(36x24mm，即传感器尺寸)的镜头焦距指代视场角度。（即等效焦距）

17mm广角104°
50mm中焦47°
200mm长焦12°

曝光

H = T x E
曝光 = 时间 x 辐射度
时间由快门(shutter)控制
辐射度影响因素
- 落到传感器单位面积上的光强
- 光圈(aperture)大小与焦距

ISO

简单理解为感光元件信号放大。线性成正比。

F-Number：曝光等级

焦距除以光圈直径。可通俗理解为光圈直径的倒数。

快门

一些基础的知识包括运动模糊
快门拉开过程速度的副作用：Rolling shutter
- 由于快门打开存在过程，导致实际照片各部分在不同的时间采样，高速运动物体出现扭曲
- PS：这其实不仅是机械快门的原因。电子快门而言CMOS按行写信息也会导致各像素采样时间的偏差

薄透镜的近似 Thin Lens Approximation

我们对现实情况做一个近似，不考虑透镜组以及复杂透镜的像差(aberrations，光线未聚焦到一点)情况。

理想薄透镜
- 所有进入透镜的平行光线穿过焦点
- 所有穿过焦点的光线在穿过透镜后平行
- 焦距可被任意改变（现实中透镜组可实现这一理想）

焦距、物距、相距关系，高斯薄透镜公式(Gaussian Thin Lens Equation)（初中物理回顾） $$ \frac{1}{f} = \frac{1}{z_i} + \frac{1}{z_o} $$

计算弥散圆尺寸 Computing Circle of Confusion (CoC) Size

透镜成像时存在一个焦平面，焦平面上的物体能清晰地成像在感光元件上。但远离焦平面的物体会成像在像平面前，从而最终打在感光元件上成为一个“弥散圆(Cricle of Confusion)”，圆内像素无法分辨光线的来路。弥散圆尺寸与光圈大小成比例。$z_i$像距，$z_s$感光元件到透镜距离，$d^\prime$感光元件到像的距离。 $$ \frac{C}{A} = \frac{d^\prime}{z_i} = \frac{|z_s - z_i|}{z_i} $$

景深 Depth of Field

景深即为CoC足够小（e.g. 小于一像素）的一个成像平面范围。

L20 颜色与感知 Color and Perception

光场 Light Field / Lumigraph

全光函数 The Plenoptic Function

$$ P(\theta, \phi, \lambda, t, V_x, V_y, V_z) $$ 以此重建任意位置光场

光场是从任意位置向任意方向的光强度。四维表示。可以使用两个平面描述，各取一点确定一条光线。

光场相机

将像素替换为透镜，形成微透镜阵列(Microlens array MLA)，记录光场（各个像素点上不同方向的光强）信息，从而可以通过计算后期重聚焦、调整光圈大小。

颜色的物理基础 Physical Basis of Color

光的电磁波性质
可见光光谱400nm - 700nm

谱功率密度 Spectral Power Distribution

光在不同波长的强度

颜色的生物基础 Biological Basis of Color

颜色是人类的一种感知。

感光细胞 Retinal Photoreceptor Cells
- 视杆细胞 Rods
  - 在低光状态下的主要感知细胞（scotopic conditions）
  - 120M
  - 感知灰度，不感知颜色
- 视锥细胞 Cones
  - 在典型光照下的感知细胞（photopic）
  - 6-7M
  - 三种不同类型，分别对应三种不同光谱敏感性
    - S：短波长，主要敏感红色
    - M：中波长，主要敏感黄色
    - L：长波长，主要敏感蓝色
  - 提供颜色感知

研究表明，每个人的视锥细胞类型分布很不一样。暗示每个人的看到的颜色并不一样，看到的世界也不一样。我多年的疑虑并不是多余的。

人最终感受到的是谱功率密度在三种视锥细胞上积分得到的结果(S, M, L)。

同色异谱 Metamerism

我们呈现颜色的基本原理。只要最终积分得到的结果(S, M, L)一样，我们就会看到一样的颜色，无需重现原本的谱功率密度的光。

颜色混合 Color Reproduction / Matching

加色 Additive Color

给定一组基础光，各有不同的光谱分布
调整这些光的亮度并相加
颜色便被三个标量描述

就是RGB了。

需要注意的是这里允许标量是负的，实际是在被测颜色中加上负标量对应量的分色。

色彩空间 Color Space

标准RGB sRGB

制作特定显示器RGB标准
其他颜色设备通过校准模拟该显示器
广泛使用
色域有限

全局色彩空间 CIE XYZ

一套人造的色彩标准，想象的标准色XYZ
- 不存在符合这套匹配函数的标准色
- Y是亮度 (Luminance)
设计目的
- 匹配函数严格正
- 覆盖所有可见光

Separating Luminance, Chromaticity

将XYZ归一化为xyz，固定Y，使用xy绘图描述色域。

CIE Chromaticity Diagram

色域中心为白色。

感知组织颜色空间 Perceptually Organized Color Space

HSV颜色空间 Hue-Saturation-Value
CIELAB Space
- 轴两端为互补色（互补色的两个实验很强很有意思，之前好像见得不多）

减色

CMYK，K黑色出于成本考虑。

L21 动画 Animation

顺序查看顺序图像产生运动效果。

一些常见帧率
- 电影：24fps
- 一般视频：30fps
- VR：90fps

关键帧动画

在keyframes中插值。

物理模拟 Physical Simulation

基于牛顿第二定律$F=ma$，使用数值模拟生成物体运动。

动态系统建模示例：质点弹簧系统 Example of Modeling a Dynamic System: Mass Spring System

一个简单的弹簧

理想弹簧$f_{a\rightarrow b} = k_s(b-a)$。引入原长使得弹簧本身有长度。

引入能量损失

理想弹簧会简谐运动不停。再引入摩擦力以避免弹簧永远震动。

一个简单的运动阻尼(motion damping) $f = -k_d \dot{b}$

表现为对运动的一个粘性拖拽(viscous drag on motion)
在速度方向上减慢运动
不足
- 会减慢所有的运动
  - 弹簧落向地面，此时应该产生该阻尼么？

我们想要的阻尼应该只阻碍弹簧内部由弹性产生的运动。

该阻尼只由弹簧两端点相对速度决定
相对速度对阻尼大小的影响与相对速度的方向也有关
- 考虑以一端点为中心另一点做圆周运动，此时不应受阻尼影响
- 将相对速度做在弹簧上的投影以考虑弹簧的拉伸变化情况

改进得到一种适用的阻尼表达： $$ f_b = -k_d\frac{b-a}{\|b-a\|}(\dot{b} - \dot{a})\dot \frac{b-a}{\|b-a\|} $$

注意：这只是一种特定的阻尼类型。

弹簧组成结构

尝试用弹簧模拟布料。简单网格有以下缺陷：

无法抵抗切变(shear)：对角拉扯会收缩
无法抵抗平面外的力：可以被完美对折

做以下改进：

对角线增加弹簧连接抵抗切变
通过间隔端点的弹簧连接抵抗对折

粒子系统

基础介绍

(正向)运动学 Forward Kinematics

被铰接的骨架 Articulated skeleton
- 拓扑连接关系
- 连接关节的几何关系
- 树形结构
关节类型 joint types
- Pin 1维旋转
- Ball 2维旋转
- Prismatic joint 允许平移
优点
- 容易直接控制
- 实现简单
缺点
- 动画与物理现实不一致
- 对艺术家来说比较耗时

逆向运动学 Inverse Kinematics

已知端点位置，求解骨骼姿态。

一般N-link逆运动学问题的数值解法

选择初始配置
定义误差度量
计算误差梯度
应用梯度下降或牛顿法等优化方法求解

绑定 Rigging

对角色的一系列高阶控制，使得对姿态、变形、表情等控制更快速、更符合直觉。

形状调和 Blend Shapes

直接插值面而不是骨骼。如建模一系列面部表情。最简单的，线性组合顶点位置，使用样条(spline)控制各时间的权重。

动作捕捉 Motion Capture

优势
- 快速捕捉大量真实数据
- 高度真实感
劣势
- 复杂昂贵的场景
- 捕捉的动画可能不能满足艺术需要，需要调整

L22 动画 Animation (Cont.)

单粒子模拟 Single Paritcle Simulation

假设已知任意时间与位置的速度，即拥有一个速度场，可表示为$v(x,t)$。可通过解一个一阶常微分方程(Ordinary Differential Equation ODE)得到粒子在不同时间的位置。

$$ \frac{dx}{dt} = \dot{x} = v(x, t) $$

欧拉方法 Euler’s Method

又名前向欧拉，显式欧拉。

简单的迭代法
广泛运用
非常不准
大多数情况下不稳定

$$ x^{t+\Delta t} = x^t + \Delta t\dot{x}^t \\ \dot{x}^{t+\Delta t} = \dot{x}^t + \Delta t \ddot{x}^t $$

完全使用上一时刻的量来估计下一时刻的状态。误差会随着数值积分而累积。欧拉方法积分尤其不好。 这可以通过使用小步长来缓解。

考虑一个圆周速度场。完美情况下粒子作圆周运动。但任意步长下的显式欧拉方法都会使得例子向外螺旋飞出。这表明显式欧拉法的误差存在正反馈，越来越大。稳定性方面存在两个关键问题：

步长增加，精确度下降
不稳定性是一个常见、严重的问题导致模拟发散

误差与不稳定 Error and Instability

通过有限差分解决数值积分导致两种问题：

误差
- 误差随着迭代累积，精确度越来越低
- 误差在图形学应用可能并不关键
不稳定性
- 误差会复合(compound)，导致模拟发散，尽管真实系统并不会
- 缺少稳定性是基础问题，不可忽视

对抗不稳定 Combat Instability

中点法 Midpoint Method

计算欧拉步骤(Euler step)
在欧拉步骤的中点计算导数(derivative)
使用中点导数更新位置

$$ x_{\text{mid}} = x(t) + \Delta t/2 \dot v(x(t), t) \\ x(t+ \Delta t) = x(t) + \Delta t \dot v(x_{\text{mid}}, t) $$

自适应步长 Adaptive Step Size

基于误差估计选择步长的技术
非常实用
可能会需要很小的步长

重复以下步骤直到误差小于阈值：

计算欧拉方法步骤，步长T
计算两次欧拉方法步骤，步长T/2
计算以上两次结果误差
如果误差大于阈值则减小步长并重试

隐式欧拉方法 Implicit Euler Method

使用下一时刻的速度与加速度来计算当前步骤。使用解析解或牛顿法求解。提供很好的稳定性。 $$ x^{t+\Delta t} = x^t + \Delta t\dot{x}^{t+\Delta t} \\ \dot{x}^{t+\Delta t} = \dot{x}^t + \Delta t \ddot{x}^{t+\Delta t} $$

衡量稳定性

衡量方法
- 局部截断误差(local truncation error)：每一步的误差
- 整体累计误差(total accumulated error)：整体误差
绝对数值并不重要，阶(order)是需要关心的
隐式欧拉法拥有1阶误差
- 局部截断误差$O(h^2)$
- 全局累积误差$O(h)$
- h指步长
- 意味着步长减半，全局误差减半

龙格库塔方法 Runge-Kutta Families

指一类解决常微分方程的高阶方法

非常善于处理非线性
四阶版本被广泛使用，即RK4

初始情况 $$ \frac{dy}{dt} = f(t, y),\ y(t_0) = y_0 $$

RK4 solution $$ y_{n+1} = y_n + \frac{1}{6}h(k_1 + 2k_2 + 2k_3 + k_4) \\ t_{n+1} = t_n + h $$

where $$ \begin{aligned} k_1 = f(t_n, y_n) \\ k_2 = f(t_n + \frac{h}{2}, y_n + h \frac{k_1}{2}) \\ k_3 = f(t_n + \frac{h}{2}, y_n + h \frac{k_2}{2}) \\ k_4 = f(t_n + h, y_n + hk_3) \end{aligned} $$

基于位置的/魏莱积分 Position-Based / Verlet Integration

思想
- 在改进欧拉法之后，约束粒子位置来防止发散、不稳定行为
- 使用约束位置来计算速度
- 这些思想都会损失能量，稳定
优缺点
- 快速简便
- 不基于物理，损失能量导致误差

刚体模拟 Rigid Body Simulation

类似粒子模拟
只需要多考虑一些属性

$$ \frac{d}{dt} \begin{pmatrix} X \\ \theta \\ \dot{X} \\ \omega \end{pmatrix} = \begin{pmatrix} \dot{X} \\ \omega \\ F / M \\ \Gamma / I \end{pmatrix} $$

X: 位置
$\theta$：旋转角度 (rotation angle)
$\omega$：角速度 (angular velocity)
F：力
$\Gamma$：扭矩 (torque)
I: 转动惯量（momentum of inertia）

流体模拟 Fluid Simulation

Position-Based Method

不是基于物理的模型关键思想：

认为水由刚体小球组成
假设水不可压缩
任何位置小球密度的改变需要被通过改变粒子位置“修正”
需要知道任意位置的密度梯度，该梯度与粒子位置有关
通过梯度下降更新

拉格朗日方法与欧拉方法 Eulerian vs. Lagrangian

又见面了。草草地复习。

拉格朗日质点法
欧拉网格法

物质点法 Material Point Method (MPM)

混合方法，结合欧拉法与拉格朗日法。

拉格朗日部分：认为粒子携带物质属性
欧拉部分：使用网格进行数值积分
交互：粒子转移属性到网格，网格更新后插值回粒子

完结

张无忌学完之后，张三丰问：还记得吗？
张无忌答：全都记得
过了一会又问：现在呢？
无忌答：已经忘却了一小半。
又一会，答：啊，已经忘了一大半。
到最后：已经全都忘了，忘得干干净净。

回到一切的开始。计算机图形学大致四部分内容：

光栅化
几何
光线传播
动画/仿真

光栅化的内容教得差不多了。几何的路还很长。光线传播后面还有课可以听，包括实时光线追踪。仿真之后有胡的课，猜测应该是和胡的work太极关系紧密。看着太极起步到发展，效果确实很好，给GPU编程搭了类似Python的普及化桥梁，做了各种优化，感觉很适合上手，但不知道工业应用怎么样。

路漫漫其修远兮。